ブラック・ショールズ・モデル
ストック・オプションの公正価値算定手法としても最も有名なのがブラック・ショールズ・モデル(BS式)と言えます。
会計基準上も、企業会計基準適用指針第11 号「ストック・オプション等に関する会計基準の適用指針」(以下「適用指針」という。)に下記記載があり、BS式が実務で広く適用されている算定技法として挙げられています。
株式オプション価格算定モデル
「適用指針」第2項
2. 本適用指針における用語の定義は次のとおりである。
(1) 「離散時間型モデル」とは、株式オプション価格算定モデル等の株式オプション価値の算定技法のうち、将来の株価の変動が、一定間隔の時点において一定の確率に基づいて生じると仮定する方法をいう。離散時間型モデルの典型例として、1 期間後の株価が一定の確率に基づいて上昇するか下落するかの2 つのケースのみを想定する二項モデルがある。
(2) 「連続時間型モデル」とは、株式オプション価格算定モデル等の株式オプション価値の算定技法のうち、将来の株価の変動が、一定の確率的な分布に基づいて常時連続的に生じると仮定する方法をいう。連続時間型モデルの典型例として、ブラック・ショールズ式がある。
ブラックショールズ方程式を確立したショールズとマートンは1997年にノーベル経済学賞を受賞しており(ブラックはその2年前に逝去)、その導出課程は数学的に複雑なため専門書にゆずりますが、ストック・オプション評価の実務においてよく使われる最終形の計算式としては下記が一般的です。
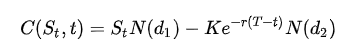
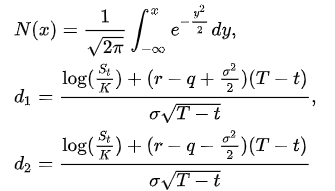
一見すると複雑な計算式ですが、BS式を反映したEXCELフォーマットもネット上で公開されており、必要なパラメータがあれば誰でも計算できることも特徴として挙げられます。
ブラック・ショールズ・モデルによる価値算定のパラメータ
BS式のオプション価値算定にあたり考慮すべき主なパラメータは以下の通りです。
| パラメータ | 概要 | 設計可能性 |
| 行使価格 | SO行使時の払込額 | 設計可 (実務上は株価と同一にすることが多い) |
| 満期までの期間 | SO行使可能期間 | 設計可 |
| 株価 | SO価値算定時点の株価 | 所与 |
| 株価変動性 (ボラティリティ) | 将来の株価変動性 | 所与 |
| 配当率 | 満期までの期間における 想定配当率 | 所与 |
| 無リスク利子率 | 権利行使期間までの期間に対応する リスク・フリー・レート (国債利回り等) | 所与 (満期までの期間により変動) |
ブラック・ショールズ・モデルのパラメータと評価結果との相関
BS式の各パラメータが増減した場合において、その増減がSO評価にどのように影響を与えるかの相関関係を整理すると下表のようになります。
| パラメータ | SO評価への影響 | パラメータ増減とSO評価の相関 |
| 行使価格 | 行使価格の増加 ↓ SO評価額は下がる | 行使価格の増加は将来獲得するキャッシュ(純額)の減少につながるため、SO評価が下がる。 |
| 満期までの期間 | 満期までの期間の延長 ↓ SO評価額は上がる | 行使期間が長くなるほど将来獲得するキャッシュが増加する可能性が高くなるため、SO評価が上がる。 |
| 株価 | 算定時株価の上昇 ↓ SO評価額は上がる | 例えば株価100・行使価格100のSOにつき株価のみ150に増やすと、SO付与の時点でイン・ザ・マネー(即行使したら50の含み益状態)となるため、SO価値としては高いものとみなされる。 |
| 株価変動性 (ボラティリティ) | 将来の株価変動性の上昇 ↓ SO評価額は上がる | 株価変動性が上昇するということは、将来の株価変動が大きくなる前提を設けることであり、大きな株価変動においては大きなキャピタルゲイン(ペイオフ)が達成される可能性が高くなるため、SO価値が増加する関係性となる。 |
| 配当率 | 配当率の上昇 ↓ SO評価額は下がる | SO所有者としては配当受領権を有さないため、将来配当率を高めると配当権利落ちの状況がより顕著となり、株価下落につながる考え方においてSO価値が減少する |
| 無リスク利子率 | 無リスク利子率の上昇 ↓ SO評価額は上がる | 直感的にわかりづらいものの、将来キャッシュフローの割引率である無リスク利子率が上昇すると、割引後の権利行使価格が(計算上は)下がる結果となり、行使価格の減少がSO評価の増加につながるものと考える |
二項モデル
二項モデルも、ブラック・ショールズ・モデル(BS式)と並んでストック・オプション公正価値の算定手法として有名です。
二項モデルの計算プロセスおよび主要な計算式は下図のようにあらわされます。
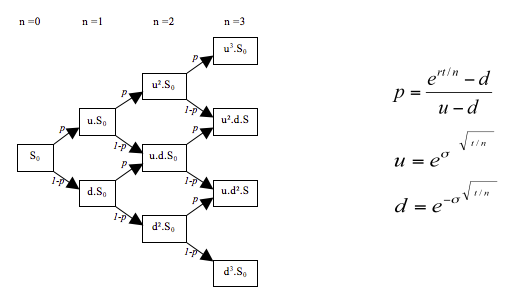
格子状の計算プロセスにおいては、時点nからオプション価値が上がる確率をp、下がる確率を「1-p」としています。そして最終格子点(上図ではn=3)でのオプションのペイオフ(≒キャピタルゲイン相当)を求めてから、現時点(上図ではn=0)まで割り引くことにより価値算定します。
会計基準上も、企業会計基準適用指針第11 号「ストック・オプション等に関する会計基準の適用指針」(以下「適用指針」という。)に下記記載があり、「離散時間型モデル」の典型例として記載されています。
株式オプション価格算定モデル
「適用指針」
2. 本適用指針における用語の定義は次のとおりである。
(1) 「離散時間型モデル」とは、株式オプション価格算定モデル等の株式オプション価値の算定技法のうち、将来の株価の変動が、一定間隔の時点において一定の確率に基づいて生じると仮定する方法をいう。離散時間型モデルの典型例として、1 期間後の株価が一定の確率に基づいて上昇するか下落するかの2 つのケースのみを想定する二項モデルがある。
(2) 「連続時間型モデル」とは、株式オプション価格算定モデル等の株式オプション価値の算定技法のうち、将来の株価の変動が、一定の確率的な分布に基づいて常時連続的に生じると仮定する方法をいう。連続時間型モデルの典型例として、ブラック・ショールズ式がある。
アメリカンタイプとヨーロピアンタイプ
ストック・オプションの権利行使時点を型で分けた場合、アメリカンタイプとヨーロピアンタイプに大別され、それぞれ下記の特徴があります。
アメリカンタイプ:
権利行使期間内であれば新株予約権者が自由なタイミングで行使可能とするタイプ
→日本企業が発行する大半の有償新株予約権における設計
→二項モデルが評価に適している
ヨーロピアンタイプ:
行使期間の満了日等、決められた一定時点で行使可能とするタイプ
→ブラック・ショールズ・モデルが評価に適しているが、二項モデルでも計算可能
連続時間型モデルと離散時間型モデル
数学的に詳細な説明は割愛しますが、ブラック・ショールズ・モデルも二項モデルも基本的な考え方は同じであり、一定の仮定に基づき将来株価が変動する前提において、原資産価値(≒SO価値)がどのように定まるかを決めるためのモデルです。
考え方の違いとしては「適用指針」にあるとおり、連続時間型モデルと離散時間型モデルのどちらをベースにしているかであり、下記のように整理されます。
連続時間型モデル:
原資産価値(≒SO価値)の変化が切れ目なく連続的に発生している前提を設けるモデル
→ブラック・ショールズ・モデルにおいて採用
離散時間型モデル:
原資産価値(≒SO価値)の変化が断続的に発生している前提を設けるモデル
→二項モデルにおいて採用
つまり、一言で表現すると原資産価値の変化が「連続的」か「断続的」かの違いとなります。そして、その証明として、離散時間型モデルである二項モデルの計算ステップ数を引き上げ、「断続」を限りなく「連続」に近づけるような計算を行った場合、理論上、二項モデルとブラック・ショールズ・モデルの計算結果はほぼ一致することとなります。
SOの予想残存期間について
上記にて計算ステップ数を上げることで二項モデルとブラック・ショールズ・モデルは近似すると記載しましたが、実際の(会計上の)評価において両者は一致しないことが多く、同条件で計算した場合、二項モデルの方が高く算定されることが一般的です。
これは主にSOの予想残存期間の考え方の違いであり、詳細は「適用指針」の該当箇所を引用するものの、結論としては下記の扱いになることが多いためです。
ブラック・ショールズ・モデル:
予想残存期間=満期までの期間の中間点
二項モデル:
予想残存期間=満期までの期間
ブラック・ショールズ・モデルの計算パラメータで見た通り、予想残存期間が長いことはSO価値の増加につながりますので、満期まで取る二項モデルの方が、中間点までしかとらないブラック・ショールズ・モデルよりSO価値が高くなる関係性が生じます。
(ストック・オプションに共通する特性の算定技法への反映)
「適用指針」
7. ストック・オプションに共通する、譲渡が禁止(又は制限)されているという特性は、次の方法により、公正な評価単価の算定に用いる算定技法に反映する。
(1) 連続時間型モデルによる算定技法を用いる場合には、第6 項(2)のオプションの満期までの期間に代えて、算定時点から権利行使されると見込まれる平均的な時期までの期間(以下「予想残存期間」という。)を用いる。
(2) 離散時間型モデルによる算定技法を用いる場合には、算定時点から第6 項(2)のオプションの満期までの期間全体の株価変動を想定した上で、株価が一定率以上に上昇した時点で権利行使が行われるなど、従業員等の権利行使等に関する行動傾向を想定する。
(ストック・オプションの予想残存期間)
「適用指針」
13. ストック・オプションの予想残存期間の見積りに際しては、次の要因を考慮する。
(1) 権利確定までの期間
(2) ストック・オプションの権利行使に関する従業員等の行動傾向(過去の実績から観察される権利行使の状況や時期、権利確定後の退職や満期時の権利失効等に関する傾向)
従業員の年齢、勤続年数、職位等によって、これらの傾向に大きな差異が認められる場合には、これらのグループごとにこの要因を考慮する。
(3) 株価変動性
14. 前項に基づき、ストック・オプションの予想残存期間を合理的に見積ることができない場合には、ストック・オプションの予想残存期間は、算定時点から権利行使期間の中間点までの期間と推定する。




